Modelling Lithospheric Drips and Delamination Events
Modelling the relative time-scales of the Rayleigh-Taylor Instability and delamination, using Underworld
Why model sub-continental gravitational instabilities?
Within the plate tectonics framework, continents are generally considered to have a much lower density than the asthenosphere below and therefore avoid the kind of recycling that the oceanic crust and lithosphere undergoes. The mantle lithosphere below some continents however can become denser than the asthenosphere when it cools to a steady-state geotherm, which is an unstable configuration. Some parts of the lower crust can also have compositions which are anomalously dense, for example forming through partial-melting or underplating and then transforming into dense eclogite.
Dense sub-continental material however will not necessarily sink in <100-1000 Ma, for example if its strength resists the downward buoyancy forces or if it is not sufficiently perturbed. Sub-continental instabilities do appear to occur, as they can be observed in tomography and their evolution (typically over ~3-50 Ma) can be inferred by variations in volcanism and dynamic topography (e.g. Sierra Nevada, Jones and Saleeby 2013). How weak must lithospheric mantle must be, in order to be recycled at this time-scale? In order to answer this, we need to be able to predict what this time-scale should be for a given set of material properties. This is well understood for the Rayleigh-Taylor Instability (RTI), which describes the growth of a perturbation through non-linear feedbacks in material thickening and thinning. Another mechanism, delamination, involves peeling away of the entire dense layer. How its time-scale compares to the RTI is unclear. This means that if dense lower crust and mantle lithosphere is predominately peeled away by delamination, then current estimates of instability time-scales using the RTI model could be under-estimated, over-estimated, or this time-scale may not significantly depend on which mechanism occurs.
Modelling instabilities with Underworld
Underworld was used to model the RTI (informally called drips) and delamination, in order to compare their fundamental time-scales (Beall et. al. 2017). To generate a drip, the only requirement is that the unstable material has a greater density than the material below (the asthenosphere) and that any non-zero perturbation to its thickness exists. In numerical modelling, the latter can generally not be prevented, due to small amounts of numerical noise. In our models, small sinusoidal perturbations are inserted at the base of the dense material, with different wavelengths, so that the growth of small perturbations of particular wavelengths can be studied in a controlled way. A simple drip / RTI Underworld example can be found here. Because drips are so easily triggered, they can be thought of as the 'default' instability mechanism. To instead trigger delamination, there are an additional two requirements: 1) a weak decollement layer should separate the dense material from the strong upper crust above, allowing a pathway for channel (Poiseuille) flow and 2) the dense material should be thinned completely in a localised region, so that the asthenosphere is connected to the decollement layer.
There are therefore two parameters (see below) which control whether dripping or delamination occurs: the viscosity contrast between the dense material and the decollement layer ($\eta'_c = \eta_c / \eta$) and the size of a finite perturbation (ignoring our additional approximately 'infinitesimal' perturbations) relative to the dense material thickness ($D' = D/L$). If $D'=1$ and $\eta'_c$ is small (we found that it should be $\eta'_c < 10^{-1}$), delamination is triggered. If $D'=0$, then dripping dominates and the growth time-scale agrees with RTI analytical solutions.
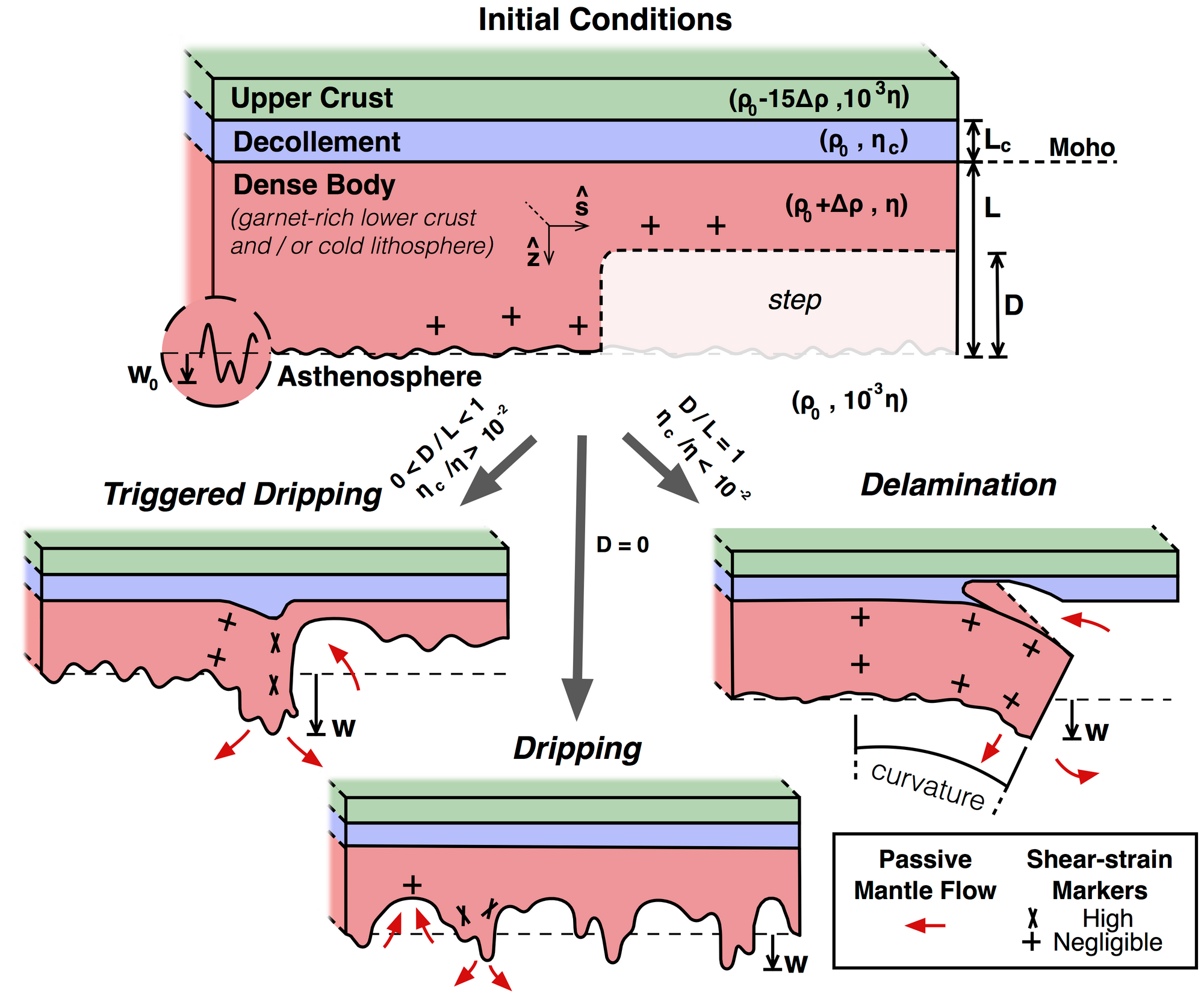
Here is a notebook, which reproduces the setup described. You can choose the values of $D'$ and $\eta'_c$ which are expected to trigger dripping or delamination and vary this. How can you actually measure if the instability in a model is more like a drip or delamination? The fundamental difference between the two mechanisms is the kind of deformation which drives their growth. Drips grow because where the dense material is slightly thickened, there exists an anomalous normal stress which drives further thickening, which in turn generates even larger stresses. Therefore dripping material needs to be able to thicken and thin, which results in significant internal shear-strain. Delamination develops because of the peeling which occurs, which involves bending of the dense material, ideally with no thickening and no internal shear-strain.
Shear-strain is measured on particles inside the dense material, which are advected with flow. Specifically, we measure the shear-strain in an orientation parallel to what would be the neutral axis in a bending beam. In the Euler-Bernoulli theory of slender bending beams, there should be no shear-strain in that orientation. The particles in the example notebook contain vectors which are initially shaped like crosses in the schematic above. At each time-step, the shear-strain is calculated at each particle location, projected onto the vectors, which are then rotated (see below). In the delamination end-member, the vectors rotate, but remain orthogonal. For dripping, many of the vectors are sheared so much that they are sub-parallel.
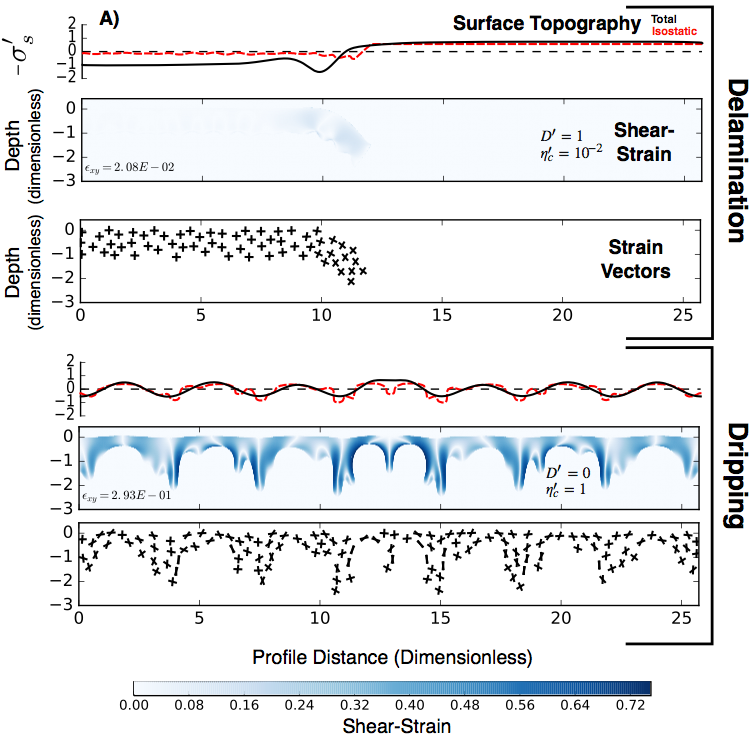
It is now worth asking - if we trigger an instability with $D'>0$ and values of $\eta'_c$ and $D'$ which do not quite trigger delamination (for example $D'<1$$ or $\eta'_c > 10^2$), how much would the deformation of the dense material still 'look' like delamination? Using $D'=0.5$ and any choice of $\eta'_c$, the shear-strain is significantly less than the dripping end-member. This can be reproduced in the notebook example. The low shear-strain can partly be explained by the large wavelength of the step perturbation, but is still smaller than expected for a drip with a large wavelength. This bending results in similarities between this mixed mode of instability, which we refer to as `triggered dripping', and delamination (shown below). Slightly more thickening and shear-strain can be measured in the modelled mixed case, compared to delamination, but it would be difficult to tell these two mechanisms apart in tomography:
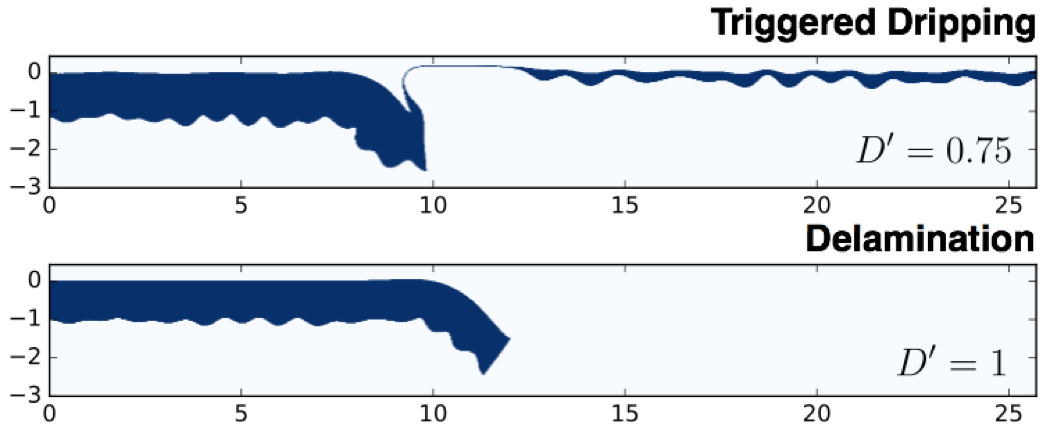
Measuring instability growth time-scales
Our aim is to quantify the relative growth time-scales of drips, delamination and the mixed 'triggered dripping' mechanism between. The sinking velocity of a drip growing from a small perturbation increases exponentially through time. The Underworld models confirm that this is the case for delamination too. A measurement of the instability time-scale therefore has to capture the exponential rate of velocity increase, rather than the velocity at a particular time (though the two are related). This is measured in the Underworld models by tracking the displacement and velocity of the particle which sinks to a reference displacement first.
See this tutorial notebook for an example of tracking the interface displacement in Underworld and measuring an exponential growth-rate.
This measurement is complicated by the presence of multiple wavelengths and a switch at high displacement to super-exponential growth. But the time-scale contrasts can be clearly captured by comparing the time it takes for the dense material to first reach a reference displacement (1L):
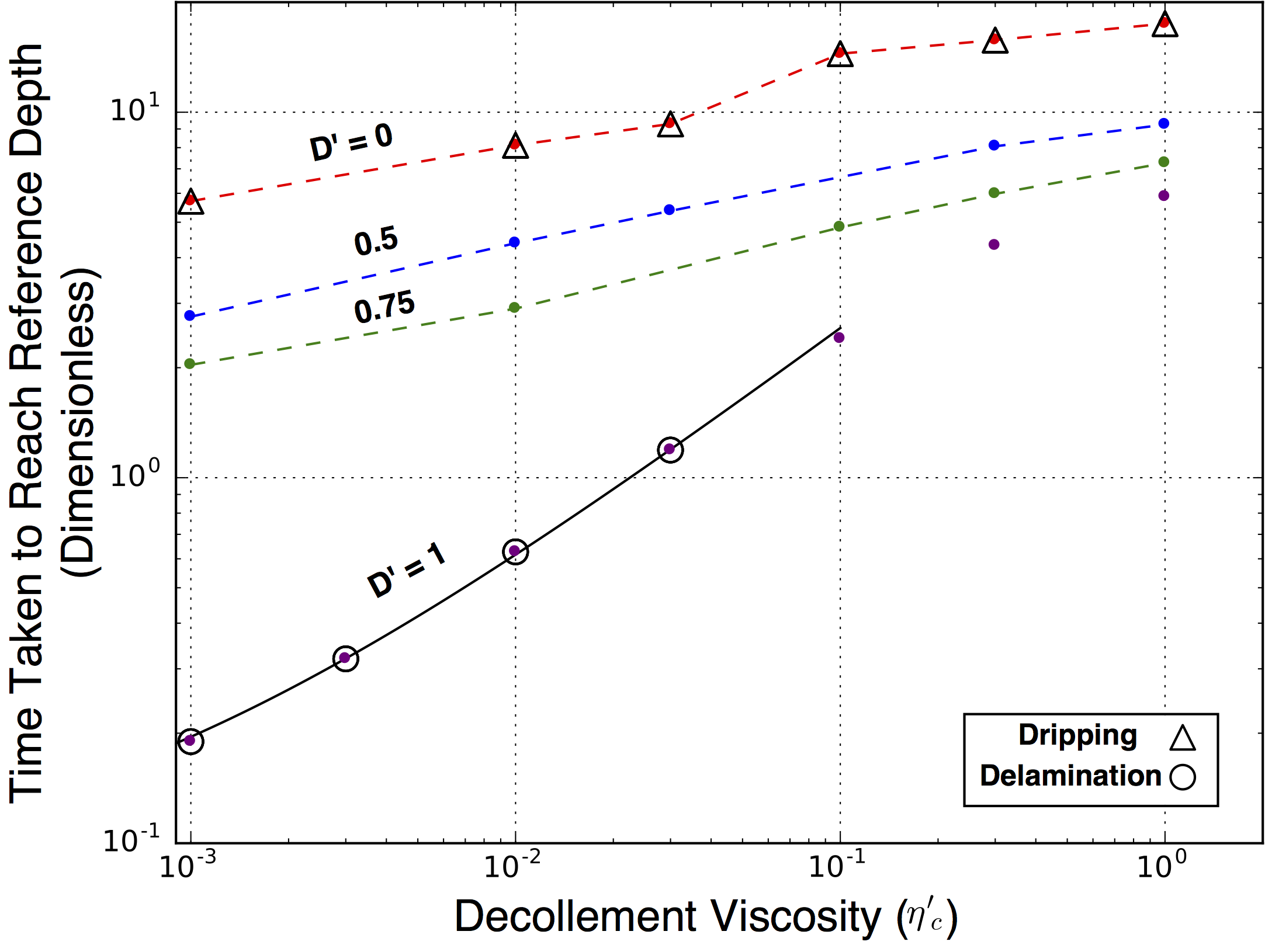
There is clearly a large spread between the times of the data points, especially considering the log scale. With dripping and triggered dripping models, a weaker decollement speeds up the instability a little, as does increasing the size of $D'$. If delamination is triggered, then a decrease in decollement strength results in a much larger decrease in the time the instability takes. For $\eta'=10^{-3}$, this results in delaminating material reaching the reference depth in one tenth of the time it would take for triggered dripping. This is a huge contrast in time-scale, especially given the instabilities begin with the same initial gravitational potential energy and the same dense material viscosity.
The instability time-scale varies proportionally to $\eta'_c$ in the same way for both dripping and triggered dripping models. These mechanisms can then both be explained by the RTI model, which is supported by similar measurements of their initial exponential growth-rates. The stronger dependence of the delamination time-scale on $\eta'_c$ can be explained using the analytic model for delamination developed by Bird (1979), where the stress required to bend the dense material is balanced by Poiseuille flow of the decollement layer. Adjusting it to our model setup results in the prediction that the exponential growth-rate should vary proportionally to ${\eta'_c}^{-\frac{2}{3}}$, which is the plotted black curve above. This agreement supports the argument that the initiation of delamination coincides with the triggering of a fundamentally different instability mechanism.
These simple models demonstrate that for a given package of dense lower crust or mantle lithosphere, regardless of its viscosity, thickness or density, the instability will evolve at a fundamentally quicker rate if delamination is triggered (requiring $D'=1$ and $\eta'_c<10^{-1}$), rather than dripping or triggered dripping. An implication is that it is near-impossible to distinguish between the triggered dripping and delamination models shown above, even though their growth rates strongly contrast. This means that two researchers could use the same time-scale data and same tomographic model of a sub-continental density anomaly, but disagree about whether triggered dripping or delamination had occurred. Using their respective models, they would then potentially disagree about the effective viscosity of the mantle lithosphere by potentially an order of magnitude.
References
Bird, P. (1979). Continental delamination and the Colorado Plateau. Journal of Geophysical Research: Solid Earth, 84(B13), 7561-7571.
Jones, C. H., & Saleeby, J. B. (2013). Introduction: Geodynamics and consequences of lithospheric removal in the Sierra Nevada, California. Geosphere, 9(2), 188-190.
Originally published at http://www.underworldcode.org on June 29, 2017.



