Seismological Models, mineral physics and spin transitions in the lower mantle
Seismological models that are just a function of depth have been developed as representations of major seismic datasets and to provide a reference for more refined studies.

The PREM model (Dzeiwonski & Anderson, 1981) utilised a large dataset of the frequencies of the normal modes of the Earth, with the addition of some body-wave constraints. The structure with depth was rendered in terms of a limited number of polynomials in radius with, e.g., a single cubic for P, S wavespeeds and density through most of the lower mantle between 760 and 2740 km depth. PREM remains the dominant model used for long-period studies in seismology.
In contrast the ak135 model (Kennett, Engdahl & Buland, 1995) was designed to fit the empirical travel times for a wide variety of seismic phases at frequencies around 1 Hz. This model is specified by a suite of control points with linear interpolation in radius. The distribution of seismic events and stations means that the empirical travel times have a northern hemisphere bias. Nevertheless, the ak135 model has proved very effective for global earthquake location and tomographic studies using body waves, and is now used by major international agencies as the standard for location. Because ak135 was designed for travel-time calculation the wavespeed profiles for P and S waves are monotonically increasing through the mantle. A density profile was assigned to ak135 by fitting normal mode frequencies whilst keeping the wavespeed fixed (Montagner & Kennett, 1996).
The PREM and ak135 models have very similar properties through the lower mantle below 700 km, but the minor differences are important when assessing compositional models for the lower mantle (e.g., Houser et al., 2020).
Advances in experimental techniques bring the measurement of the physical properties of minerals under lower mantle pressures within reach, with high intensity x-ray investigations now allowing direct measurement of density. Further, improvements in computational methods applied to crystal structures allow investigations of a wide range of temperature conditions for high pressures. The results of experimental and computational studies for individual materials generally tie together well, and extensive compilations of mineral properties have been assembled (e.g., Stixrude & Lithgow-Bertelloni, 2011). The behaviour of mineral aggregates can then be assembled from the individual properties using thermodynamic principles.
Commonly mineral physics results, or their extrapolations to Earth conditions are compared directly with the equivalent properties of seismological models, as if these are the true state of the Earth. Such a treatment does not take into account of the assumptions built into the seismological models that were not constructed for such usage. Constraints on the density distribution through the Earth are provided by the mass, moment of inertia and the lowest frequency normal modes affected by self-gravitation. The density distribution is compatible with an adiabatic state, but this is not required.
Comparisons of mineral physics and seismic models are generally made separately for P, S wavespeeds and density or equivalently for the bulk modulus (K) and shear modulus (G). There can be advantages in looking at combinations of physical parameters to examine mutual dependencies. For example, for a regular material in a single state, the effect of increasing pressure is to produce a linear relation between the ratio of the shear and bulk moduli (G/K), and pressure scaled by bulk modulus (p/K) (e.g., Kennett 2020). These combinations minimise the influence of the density distribution. Deviations from the linear behaviour indicate a change of state and an important example is provided by the impact of the spin transition in iron minerals (e.g., Lin et al., 2013; Badro, 2014).
At shallow depths, mantle minerals contain iron in the high-spin electronic state. The effect of pressure enhances the splitting energy between the orbitals in the iron atoms and so favours the low-spin state. Under the temperature conditions in the lower mantle the spin crossover transition in spin state is expected to be gradual and occur over a broad span of pressures. The behaviour for the two most significant iron-bearing minerals expected to be present in the lower mantle is rather different.
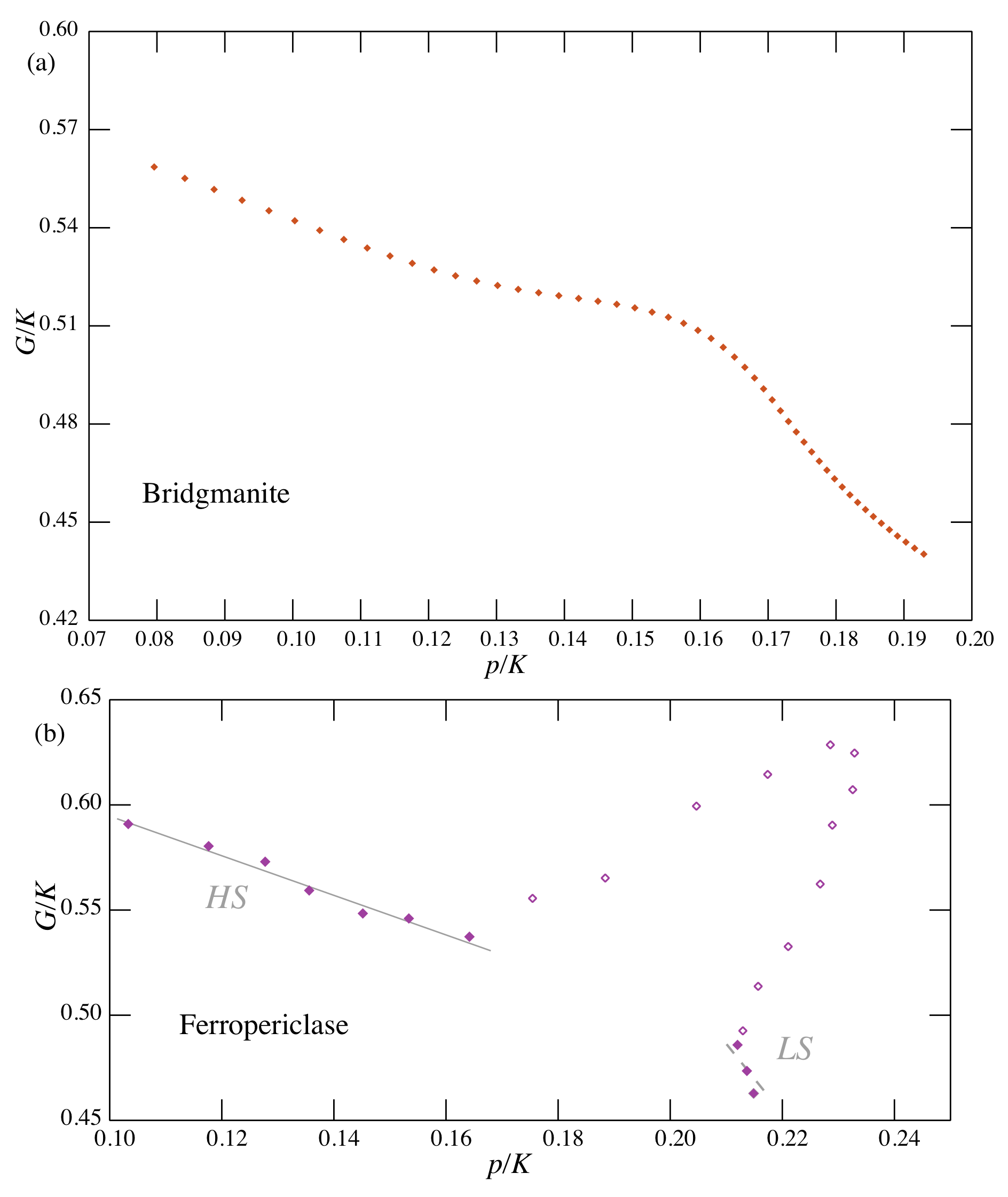
For ferropericlase (Mg1-xFexO) the spin transition is associated with ferrous iron (Fe2+), and at mantle temperatures would occur in the pressure range 50–90 GPa, accompanied by a reduction in the bulk modulus with much less effect on the shear modulus and density. The spin transition shifts to higher pressures with increasing iron content. In bridgmanite, with the perovskite structure, the situation is more complex, with the potential for different transitions depending on the valence of iron and its position in the silicate lattice structure. The net effect of the spin transition on elastic properties is quite small and can be suppressed in the presence of aluminium. The effect of the spin transition along a mantle geotherm on the ratio of elastic moduli as a function of scaled pressure is displayed in Figure 1 for both bridgmanite (without aluminium), where there is a modest effect, and ferropericlase that displays distinct high-spin and low-spin behaviour separated by the spin transition with a major excursion from linear behaviour.
Despite the expectation of noticeable changes in physical properties due to the presence of the spin transition under mantle conditions, there is no prominent feature in seismological results. The cubic polynomials spaning the lower mantle in the PREM model would not pick up a localised disturbance, and the assumption of monotonic increase in seismic wavespeed with depth in ak135 precludes the presence of a reduction in P wavespeed as expected from a reduction in bulk modulus. Nevertheless, there are indications of a change of slope in the G/K vs p/K relation for the ak135 body-wave model that is suggestive of the presence of a weak residual effect from the spin transition after 3-D averaging in the construction of the empirical travel times (Kennett, 2021).
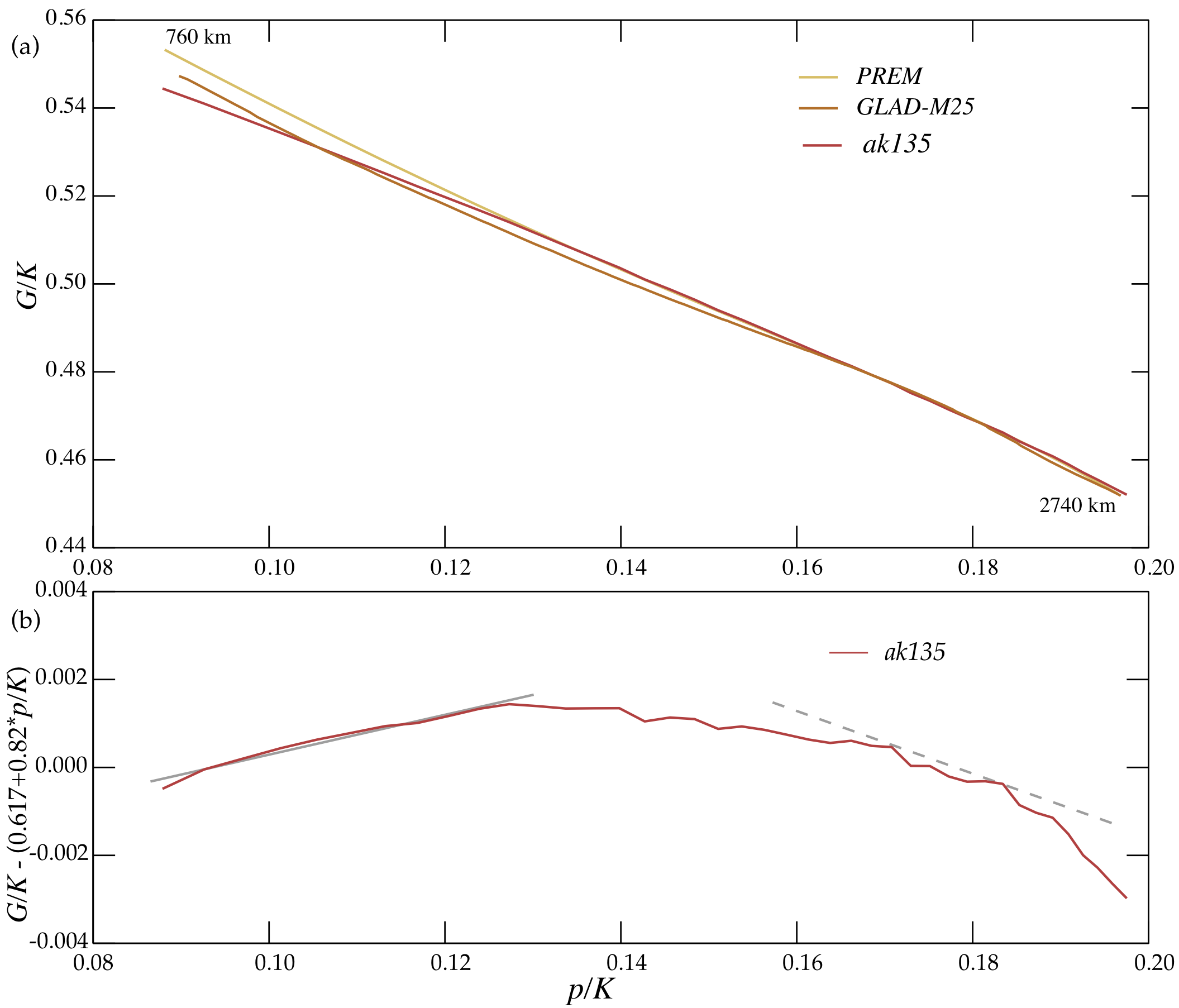
The assumption of monotonic increase in P wavespeed with depth means that the class of excursion from linearity seen in Figure 1 (particularly for ferropericlase) is not possible for ak135. But the distinct change of slope remains, as seen in Figure 2.
Recent investigations of 3-D seismic structure have used direct inversions of large portions of seismic waveforms from many earthquakes across the globe. The work of Liu et al. (2020) provides definition of P and S wavespeed in the mantle from which an estimate can be made of the spherically averaged distribution of physical properties. The results from this study are shown as GLAD-M25 in Figure 2. Although the starting point for the mantle was PREM, the tomographic model lies closer to ak135 and also displays a distinct change of slope in the G/K vs p/K relation between the shallower and deeper parts of the lower mantle.
Radial models of seismological structure represent a complex averaging of 3-D effects and carry with them a variety of implicit and explicit assumptions about the nature of the Earth. Likewise, mineral physics results bear the imprint of the sample preparation and procedures used, e.g., pressure calibration. Comparisons should be made taking into account the nature of the constraints imposed. It cannot be assumed that the seismic models represent the true Earth!
References:
Badro, J., 2014. Spin transitions in mantle minerals. Ann. Rev. Earth Planet. Sci. 42, 231–248.
Dziewonski, A.M., Anderson, D.L., 1981. Preliminary reference Earth model. Phys. Earth Planet. Inter. 25, 297–356.
Houser, C., Hernlund, J.W., Valencia-Cardona, J., Wentzcovitch, R.M., 2020. Discriminating lower mantle composition. Phys. Earth Planet. Inter. 308, 106552.
Kennett, B.L.N., 2020. Towards constitutive equations for the deep Earth II: Shear properties under pressure. Phys. Earth Planet. Inter. 307, 106558.
Kennett B.L.N., 2021 The relative behaviour of bulk and shear modulus as an indicator of the iron spin transition in the lower mantle, Earth Planet. Science Lett., 559, 116808
Kennett, B.L.N., Engdahl, E.R, Buland, R., 1995. Constraints on seismic velocities in the Earth from travel times. Geophys. J. Int. 122, 108–124.
Lin, J.-F., Speziale S., Mao, Z., Marquardt, H., 2013. Effects of the electronic spin transitions of iron in lower mantle minerals: Implications for deep mantle geophysics and geochemistry. Rev. Geophys. 51, 244–275.
Liu, W., Rouan,Y., Bozdağ, E., Peter D., Lefebvre M., Komatitsch, D., Tromp J., Hill J., Podhorszki, N., Pugmire D., 2020. Global adjoint tomography—model GLAD-M25, Geophys. J. Int. 223, 1–21.
Montagner, J.-P., Kennett, B.L.N., 1996. How to reconcile body-wave and normal-mode reference Earth models?. Geophys. J. Int. 125, 229–248.
Shukla, G., Cococcioni, M., Wentzcovitch, R.M., 2016. Thermoelasticity of Fe3+- and Al-bearing bridgmanite: Effects of iron spin crossover. Geophys. Res. Lett. 43, 5661–5670.
Strixrude, L., Lithgow-Bertelloni, C., 2011, Thermodynamics of mantle minerals – II. Phase equilibria, Geophys. J. Int. 184, 1180–1213.
Wu, Z., Justo, J.,Wentzcovitch, R., 2013. Elastic anomalies in a spin-crossover system: ferropericlase at lower mantle conditions. Phys. Rev. Lett. 110, 228501.